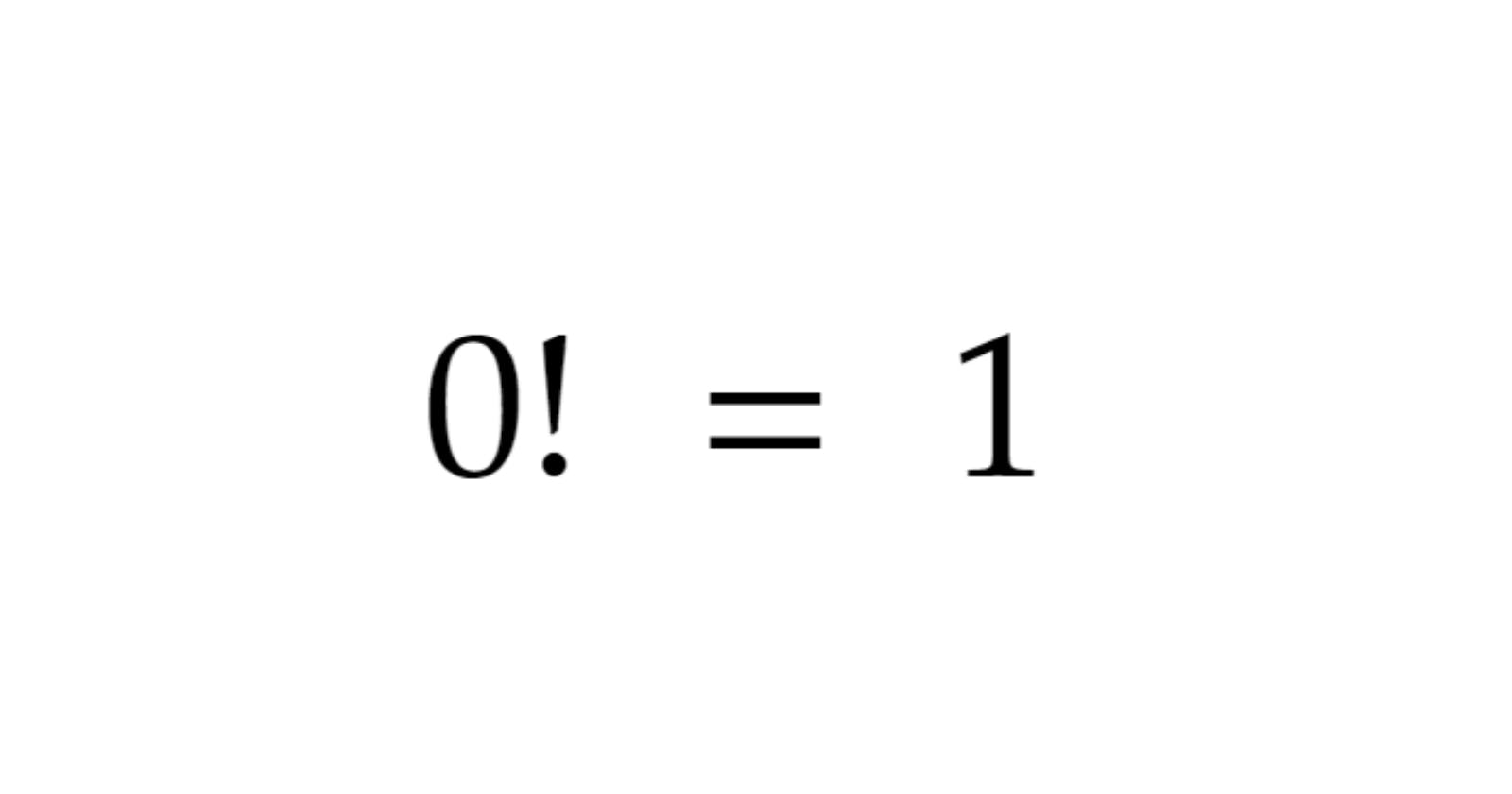Why 0! = 1

The '!' behind the 0, is notation for something called a 'factorial'.

A factorial basically tells you to take the product of all integers and itself before it until you reach 1.

If that didn't make any sense, take a look at this example.

1! = 1 2! = 1 x 2 3! = 1 x 2 x 3 4! = 1 x 2 x 3 x 4

See what I am talking about?

Now before we go to why 0! = 1, let's take a look at something called exponents and some patterns in them which will help us later on.

𝑥ⁿ (read as "𝑥 to the power of n") basically tells you that 𝑥 is multiplied by itself 'n' times, like:

2² = 2 x 2 = 4 2³ = 2 x 2 x 2 = 8

Now what do you think 2⁰ will be?

You might think that 2 multiplied by itself 0 times should be 0, but as it turns out any number to the power of 0 = 1.

2⁰ = 1, but how?

That might not make sense on first glance, but let me show you why it is correct.

Here's a list of some of the powers of 2, you'll notice a pattern over here.

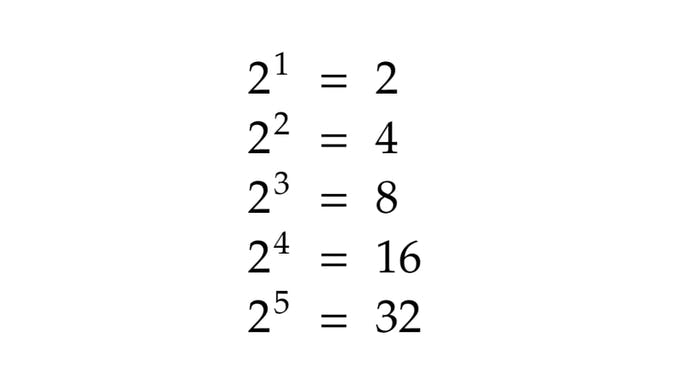
Each time you go up one level, you're essentially dividing by 2, what happens when you get to 2⁰?

You get 1, and now it all makes sense.

This is why every number to the power of 0 is 1.

(This also works for powers in negative numbers)

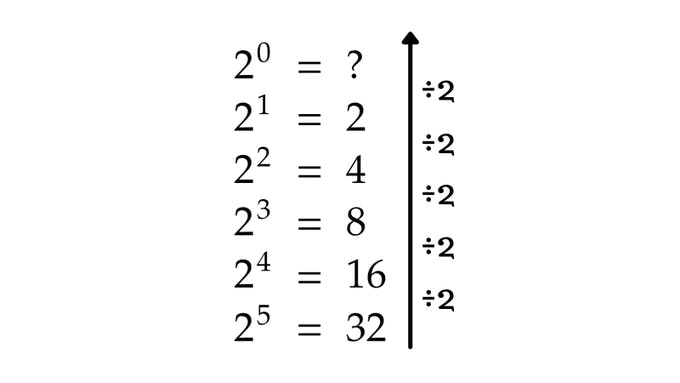
Factorials follow a similar pattern as you can see below, and as you can guess, 0! turns out to be 1 by this pattern!

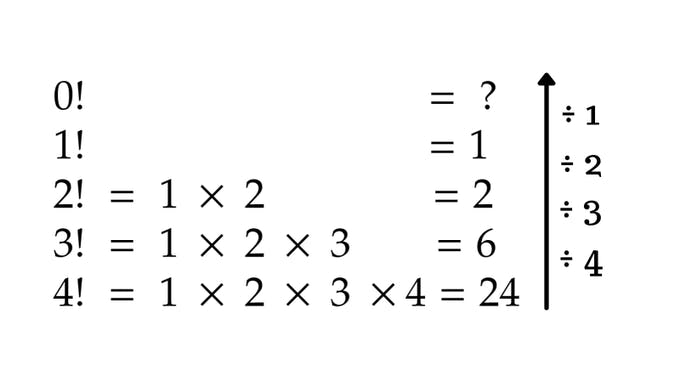
Factorials aren't just about showing a neat pattern, they have real world use cases in combinatorics, a topic in math that deals with counting.

Let me explain.

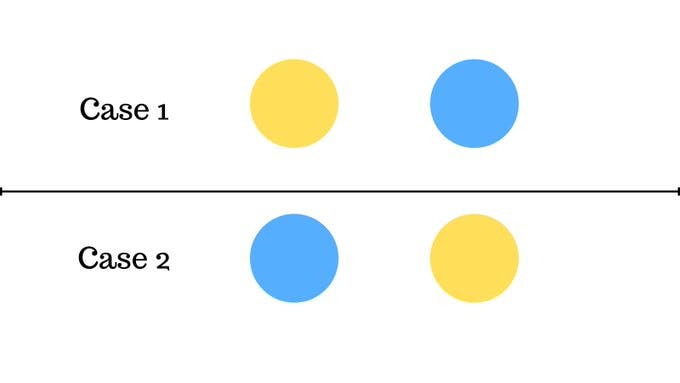
You have 2 balls, one yellow and the other is blue.

In how many different ways can you arrange them?

There are 2 possible cases, now similarly can you guess how many ways can you arrange 3 balls?

There are 6 possible cases to arrange 3 balls.

As it turns out, the number of ways you can arrange n balls is n!

2 balls = 2! = 2 3 balls = 3! = 6

2! basically means "in how many ways can arrange 2 balls" which is 2.

Now what 0! tells you is how many ways can you arrange 0 balls, or basically nothing.

There is exactly one way to show nothing!

Which again proves why 0! is 1.