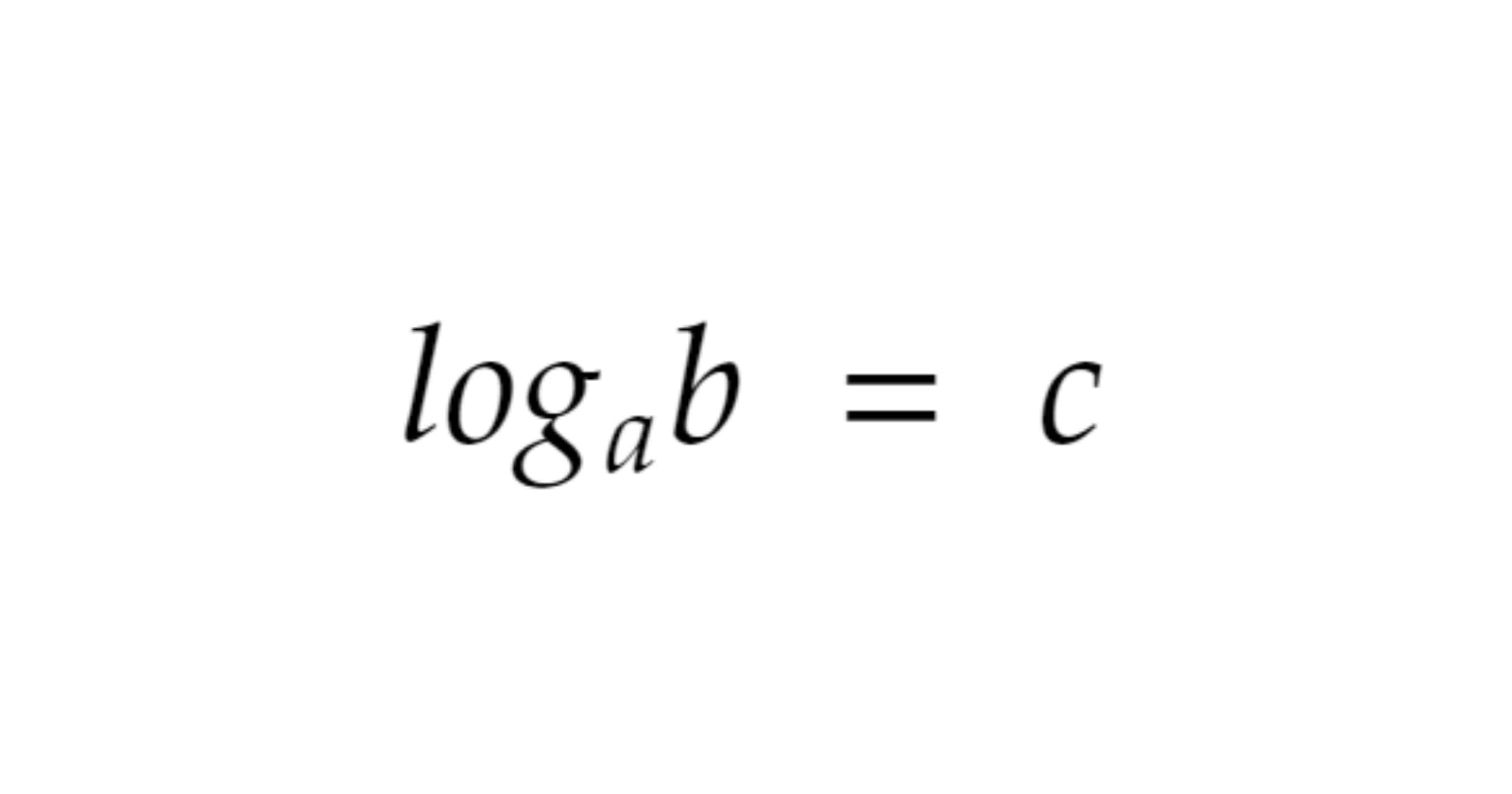Before we understand how logarithms work, it is important to know how exponents work.
aᶜ=b (read as "a to the power of c equals b") is an exponent where a,b and c are numbers.
aᶜ=b just means that a multiplied by itself c amount of times is equal to b.
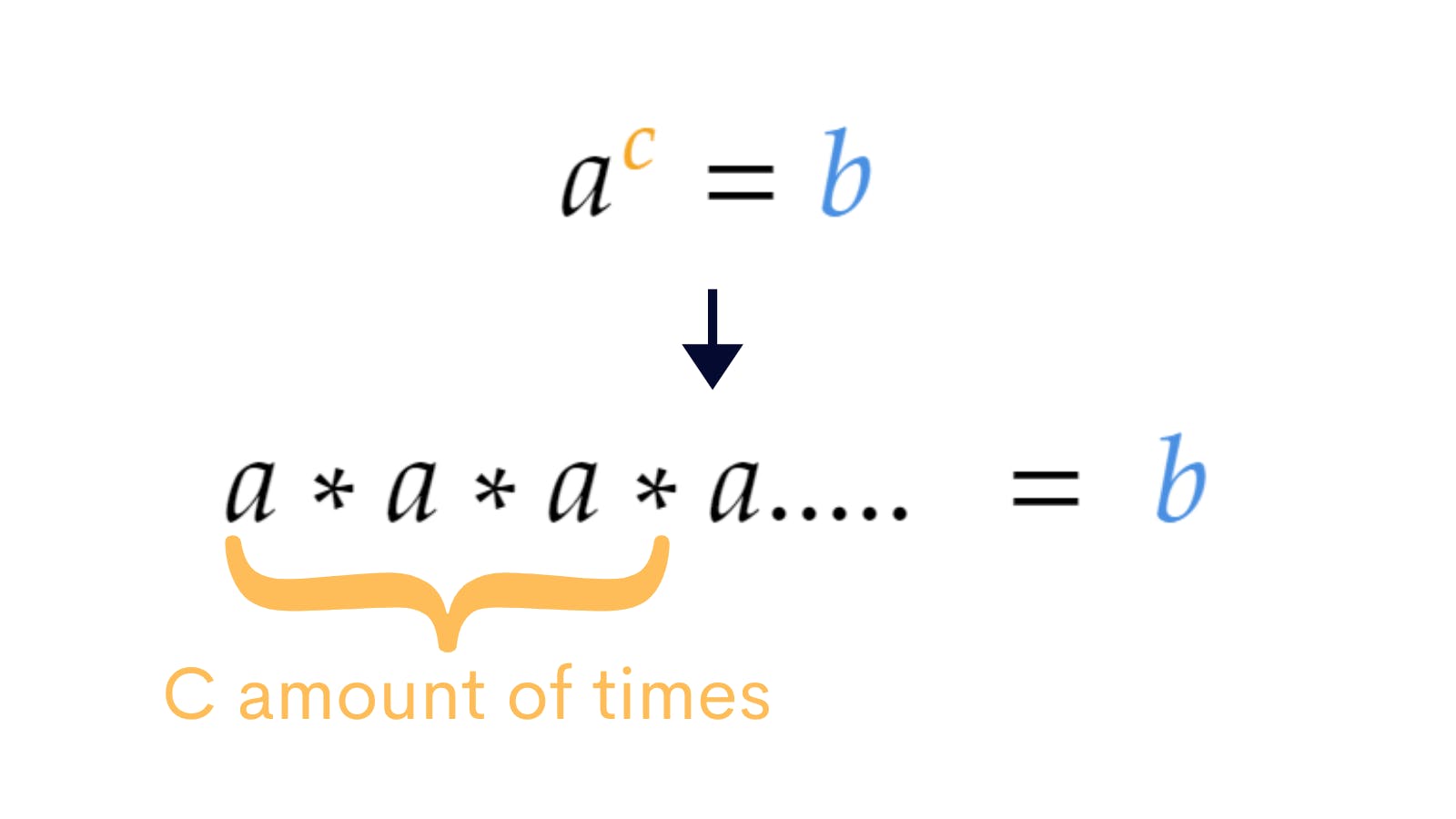
Here are some examples:
- 2² basically means 2 multiplied by itself 2 times which is 4
- 2³ basically means 2 multiplied by itself 3 times which is 8
So on and so forth.
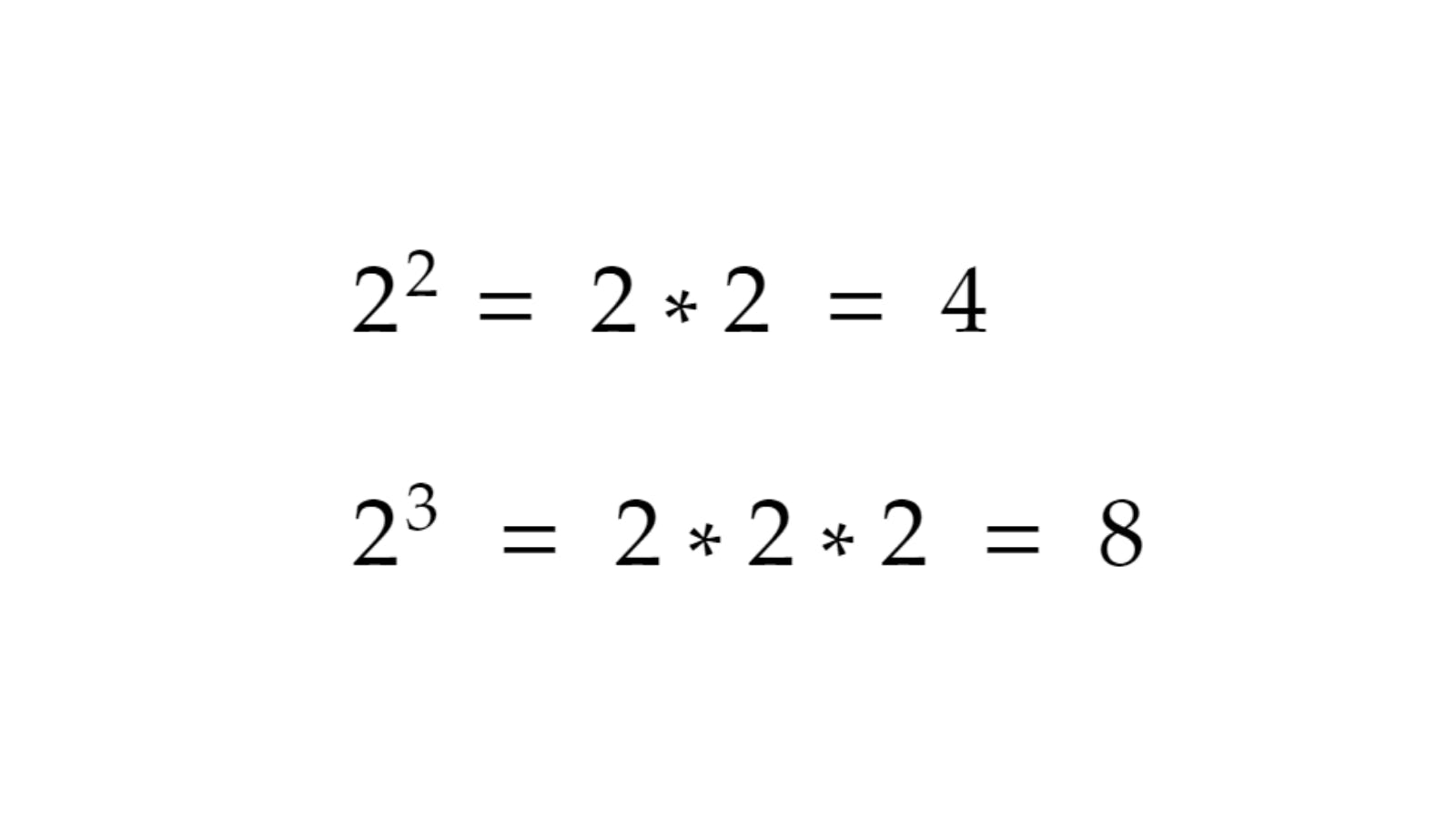
Logarithms are basically a way of representing exponents in a different format.
Let me show you what I mean, both the formulas that you see below are equal.
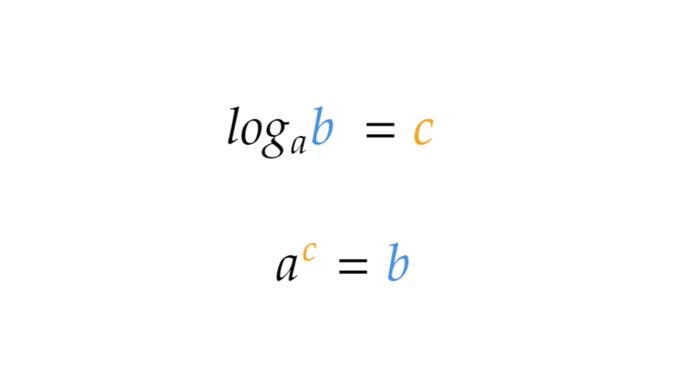
logₐb = c is basically saying that "a to the power of c = b".
Dare I say, logarithms are exponents in disguise.
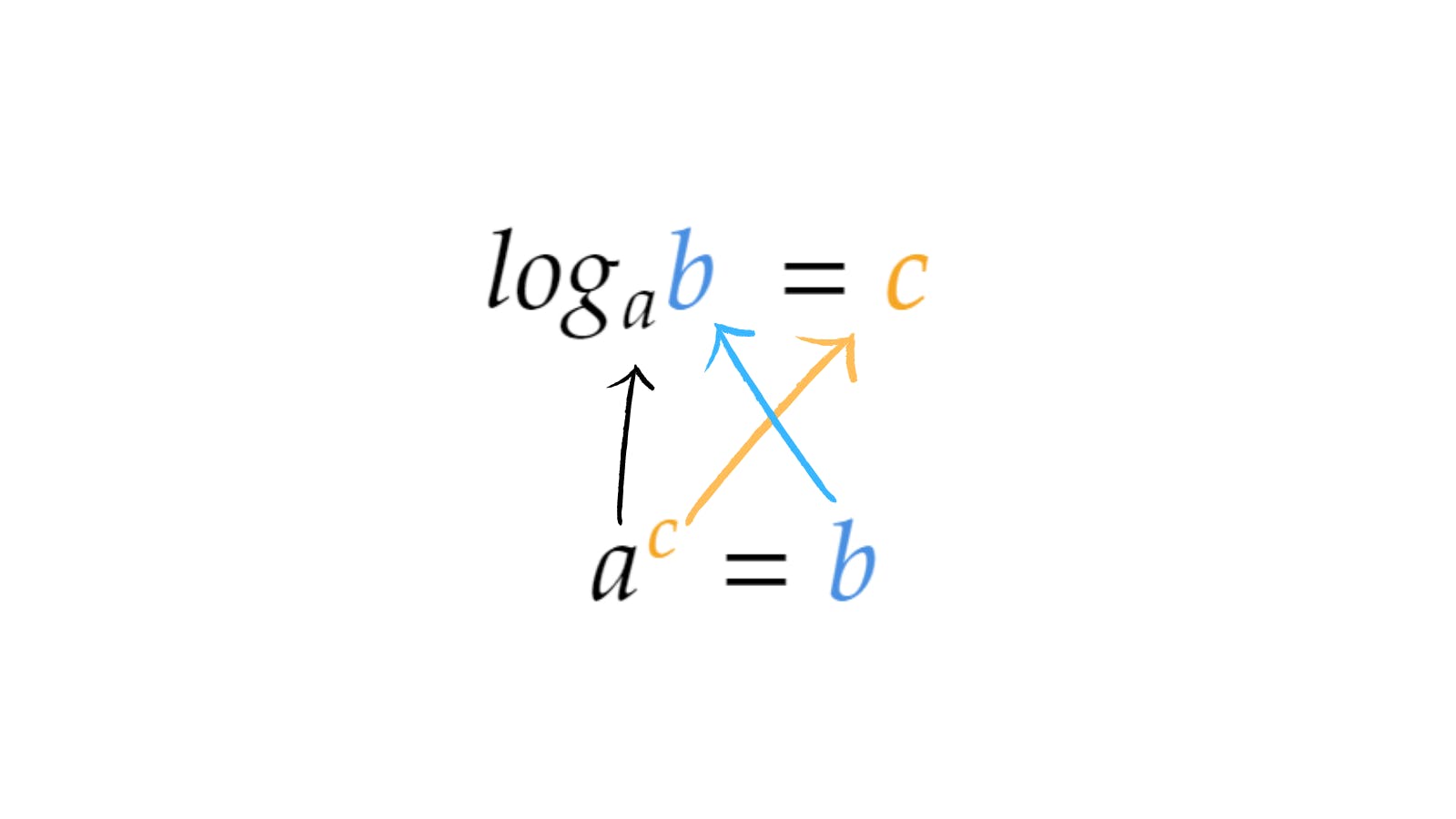
Here's a small exercise for you, what is the value of c in the below equations?
I've put them in logarithmic and exponential notation to make it easy for you.
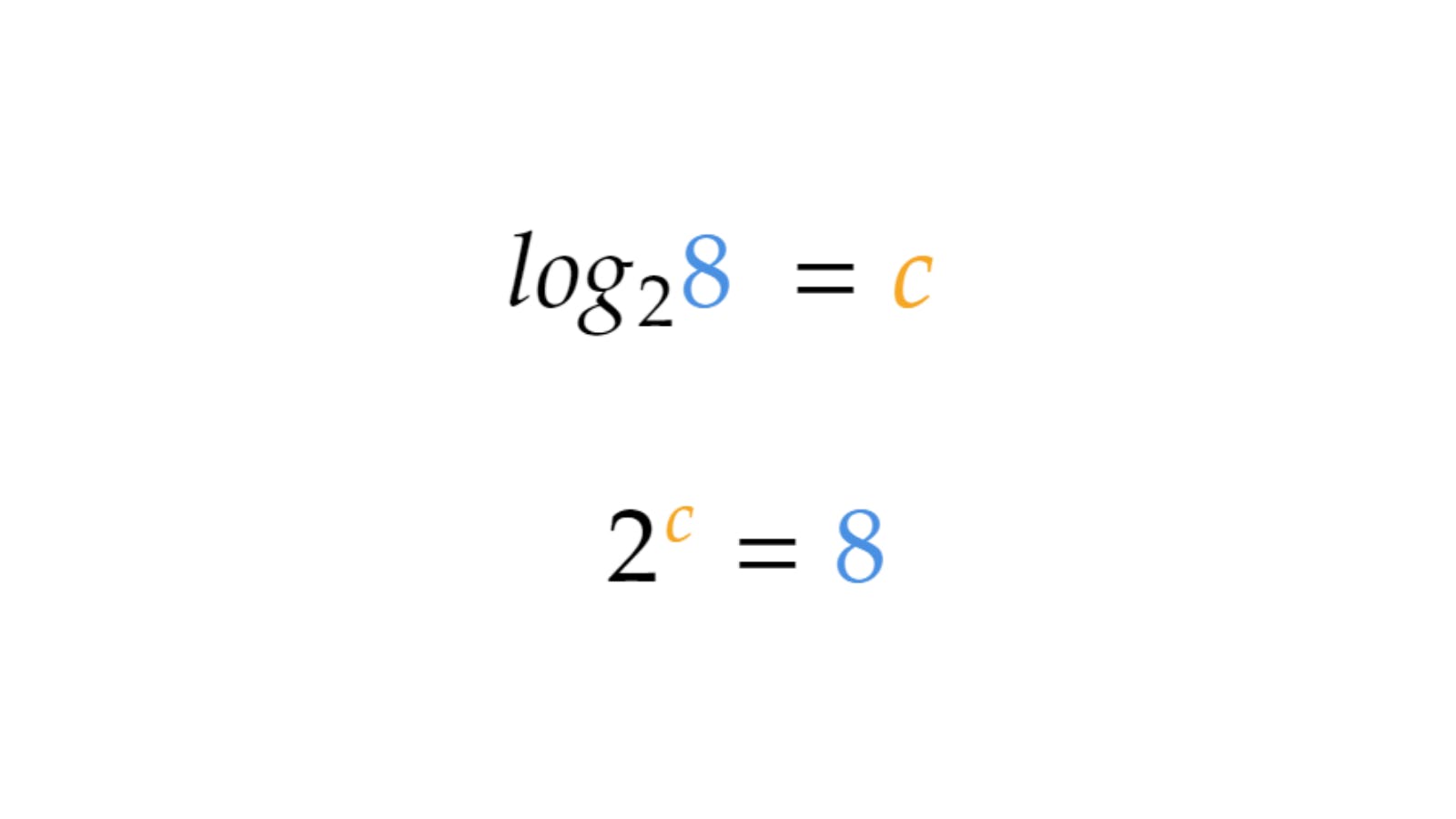
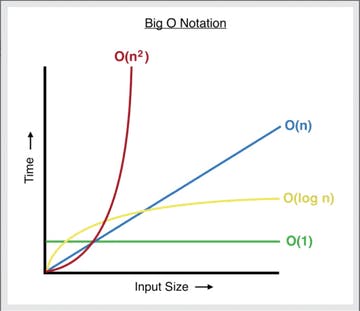
Logarithms are used in all sorts of places, machine learning, computer science (time complexities)... you name it.
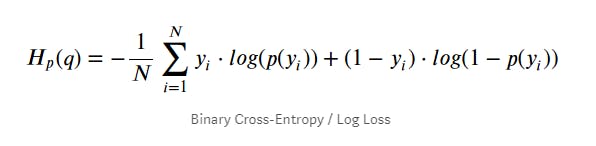
They are also a bunch of logarithmic properties that we can use to our advantage, but that is something I'll discuss in another blog post.

I really hope you enjoyed this blog post, you can also subscribe to my newsletter where I post bite-sized content like this.
Peace out!